Dédys a pour vocation d’être un outil d’inclusion, adapté aux enfants dyscalculiques et à tous les jeunes enfants, pour qui le renforcement par l’image constitue une aide à l’apprentissage.
Cet outil vise des difficultés de type dyscalculie importante pour lesquelles les enseignants sont très démunis :
- Automatisation impossible des tables (l’outil dédys permet de visualiser le résultat d’une multiplication)
- Difficulté à réaliser une opération même très simple mentalement sans soutien visuel
- Difficulté à manipuler, compter et déplacer en même temps sans erreur (dyspraxie)
Cette ressource, entièrement gratuite, a été développée grâce au soutien de la commission EduUp et duministère de l’éducation nationale, grâce également à la fondation Julien et Stella Rozan, qui décerne chaque année le prix de la coopération féminine et a récompensé Dédys en 2018. De nouvelles activités (couvrant l’ensemble du cycle 2 à terme et une partie du cycle 3) sont en cours de développement. Pour l’heure ce premier « pilote » est encore en phase de développement et d’expérimentation auprès de jeunes enfants en difficulté avec les mathématiques ou non, en lien avec des enseignants de classes ordinaires et spécialisées, ainsi que des neuropsychologues spécialisés dans les troubles des apprentissages. N’hésitez pas à tester avec vos petits élèves, en aide personnalisée, en Ulis école ou en regroupement d’adaptation et à faire retour de vos remarques à cognitice@gmail.com.
L’interface est très simple, le tableau numérique peut être utilisé. Les élèves qui auront besoin de l’appui de l’image pourront utiliser les aides visuelles affichées. Pour les plus fragiles, l’aide visuelle sera à “portée d’oeil”, en version numérique ou en pdf.
Pour avoir un aperçu de l’outil avant d’y faire un tour, une présentation en image ici.
Retrouvez toutes les activités ici. Une vraie ressource !
Tout plein d’activités mathématiques et de ressources pour le cycle 1, à découvrir ici.
Egalement à télécharger et à lire cette excellente publication sur le nombre au cycle 1.
➡ fiche_connaissance_le_nombre_C1
Maths en-vie est un dispositif qui s’appuie sur des situations de la vie quotidienne pour engager une réflexion mathématique.
Cet ouvrage présente l’ensemble du dispositif de manière exhaustive et propose 34 activités concrètes dans tous les domaines des mathématiques, pour les cycles 1, 2, 3. Elles s’insèrent naturellement dans la pratique pédagogique et la progression élaborée par l’enseignant.
L’ouvrage se compose d’un guide pédagogique, de fiches d’activités et d’un logiciel associé. Découvrez-le là.
mesures pour réformer l’apprentissage des mathématiques… De nombreux enseignants y retrouveront ce qu’ils font déjà … Téléchargez le rapport Villani/Torossian ci-dessous.
➡ Rapport_Villani_Torossian_21_mesures_pour_enseignement_des_mathematiques_896190
De nouvelles vidéos pour les maths en maternelle, sur le site de Céline Alvarez. L’ensemble du site est intéressant. C’est là.
Prévoyez une heure de votre temps pour réaliser ce module, quizz d’entrée compris… Vraiment bien.
Un générateur pour travailler la numération, le groupement par dix…
Un peu austère, mais très astucieux. Les
cubes peuvent être remplacés par des trombones, des petits sacs… On peut choisir l’écriture chiffrée ou avec le “matériel”… et l’assortir évidemment d’une vraie manipulation. Projeté au tableau, matériel sur les tables, un élève à l’ordi donne les consignes et y répond sur l’ordi….et on tourne. Autre possibilité, l’utiliser en soutien ou en remédiation…
Cette petite icône, placée en haut à droite, de la version 1 vous permet d’avoir accès à des tutoriels qui présentent des situations d’apprentissage utilisant cette appli.
Clic sur l’image pour aller voir….
9 pistes pour adapter sa pédagogie aux élèves dyscalculiques, mais aussi à tous les autres. 9 conseils avisés et aisés à mettre en oeuvre, à commencer par l’enseignement explicite.
Pour retrouver ces 9 pistes, c’est ici. D’après un ouvrage fort intéressant, parce que les pistes sont adaptables à tous les élèves, et notamment à ceux dont la procédure experte tarde un peu à s’installer…
TEMOIGNAGE (Part.2)
« Sérieux… on va jouer ! » Un article de Fabrice Bascou : Pythagore en jeu de l’oie !
Jean-Pierre Kahane écrivait en 2004 dans les Cahiers pédagogiques n °427 que «Les mathématiques ont une image sévère […] Depuis longtemps on parle de tyrannie des mathématiques, de leur pouvoir sélectif, et on les assimile à un apprentissage de l’échec».
Certes, 13 années ont passé et les choses ont évolué, mais, quand même, il y a de quoi mettre encore un peu de fun dans l’enseignement des maths !
Alors jouons… en effet «cela permet de donner ou de redonner goût et envie à l’élève» (Mathématiques et jeux au collège – Trouillot, Richard, Faradji, Le Borgne).
Je vous parlais la semaine dernière des tâches complexes qui permettent aux élèves de mobiliser les compétences mathématiques et sociales, il en est de même pour le jeu. En effet, il permet de « respecter des règles, prendre des initiatives, apprendre à coopérer, accepter de perdre […] » (ressources transversales)
Voilà plusieurs années que je feuillette la brochure jeux n° 10 de l’APMEP pour y puiser des activités mathématiques ludiques, j’y aperçois chaque année ce «jeu de l’oie» dédié à Pythagore… et je le laisse de côté…
Cette année est la bonne… je le tente!
Me voilà donc préparant mon plateau de jeu, découpant et plastifiant toutes les cartes.
J’appelle ma collègue Anne pour qu’elle vienne observer l’expérience… L’innovation pédagogique, elle ne dit jamais non !
Ne faisant pas les choses à moitié, je décide de tenter l’expérience directement en classe entière.
Voici la présentation du jeu :
Nombre de joueurs : 6 à 8 équipes de 3 à 4 élèves.
Durée d’une partie : ¾ h à 1 h (d’après la règle du jeu donnée dans la brochure)
Matériel
– un plateau de jeu projetable
– un dé à six faces
– autant de jetons différents que d’équipes et une feuille de route par équipe
– 66 cartes-questions numérotées de 1 à 66.
Présentation du jeu :
Chaque équipe reçoit un jeton et une feuille de route qui permettra de savoir quelles questions lui auront été posées et de mémoriser éventuellement son avancement. Le plateau peut être projeté au tableau (j’en reparlerai après !). Un tirage au sort donne l’ordre des équipes pour le premier lancer de dé.
Déroulement de la partie : Lorsque c’est son tour, un représentant de chaque équipe vient lancer le dé et avancer son jeton sur la case correspondante du plateau de jeu. Je donne la carte-question correspondante et coche la case associée sur la feuille de route de l’équipe. Le représentant rejoint son équipe.
Lorsque l’équipe estime avoir trouvé la bonne réponse, il envoie un représentant auprès de l’enseignant qui valide ou non la réponse. Si celle-ci est bonne, le représentant lance le dé et avance son jeton. Sinon, il retourne dans son équipe qui doit trouver la bonne réponse. La qualité de la réponse attendue (justification ou non de la réponse, par exemple) est laissée à ma discrétion, notamment en fonction du niveau des élèves de l’équipe (l’occasion de différencier se présente, profitons-en !).
Les questions sont réparties en onze séries successives de difficulté croissante, chaque série de six questions traitant d’un même type de tâches (repérer les triangles rectangles et nommer leur angle droit, citer l’égalité de Pythagore, calculer la longueur d’un côté dans un triangle rectangle,…).
Les équipes avançant indépendamment les unes des autres, la question de passer son tour ne se pose pas.
Une équipe gagne dès qu’elle a atteint l’une des six dernières cases et répondu correctement à la question posée.
Concrètement, comment s’est passée ma séance :
Mes élèves de 4èmes sont déjà répartis en îlot de 4, la séance a débuté avec l’énoncé des règles du jeu. J’avais déposé sur chaque îlot un Lego de couleur différente, couleurs associées aux Lego avançant sur le plateau de jeu. J’ai donc tiré au hasard un Lego successivement (et sans remise… les profs de maths comprendront !) pour faire débuter le jeu par chaque équipe. Cette première phase doit être dirigée de façon efficace. En effet, chaque équipe est en attente de commencer la partie, et rappelez-vous, il y en a 8 !
Une fois que chaque équipe a eu sa première carte, le jeu est officiellement lancé et les élèves étaient “comme des dingues”… J’ai eu du mal à croire qu’ils pouvaient donner autant d’énergie pour faire des maths !! Rendez-vous compte, j’ai été sollicité de la première à la dernière minute du jeu sans interruption (ndlr, c’est vrai, je suis témoin !!) ; il y avait toujours un représentant qui venait faire valider sa réponse, qui repartait, qui lançait le dé, qui redonnait sa carte, qui en reprenait une autre… (petit conseil : laisser les cartables dans le couloir !)
Les élèves se sont sans aucun doute «pris au jeu» et étaient pleinement acteurs de l’activité mathématique et en complète autonomie. De fait, la grande sollicitation des élèves, imposée par les règles du jeu ne m’a laissé aucune possibilité de les approcher au sein de leurs équipes pour peut-être donner un coup de pouce à certains ou encourager les rares petits filous qui auraient décidé de ne pas aider leurs équipes ! Si vous avez un collègue (de maths ou de français qui gère Pythagore) super sympa, demandez lui de venir jouer le rôle du maitre du jeu pour que vous puissiez circuler dans la classe.
Les règles du jeu précisent ¾ h à 1 h pour une partie… j’ai testé ce jeu sur 2 classes, et aucune n’a réussi à aller jusqu’à la fin du plateau. Comme je l’ai dit plus haut, il y a 11 séries de 6 cartes dans le jeu, je serais bien tenté de faire 11 séries de 4 cartes, ce qui donnerait un plateau de 44 cases… beaucoup plus raisonnable !
L’idée de projeter le plateau de jeu était plutôt sympa, mais a apporté de l’excitation inutile. Après avoir éteint le vidéoprojecteur dans ma deuxième classe, le niveau sonore a baissé d’un ton et la feuille de route a pris tout son sens.
En conclusion, et malgré quelques affinements à apporter, le jeu a eu l’effet escompté… un moment ludique permettant de donner une autre image des maths, des élèves mobilisés dans une activité mathématique, qui acceptent plus facilement l’aide de leurs camarades et le partage des connaissances, cela impliquant une dynamique de groupe positive.
Je vous encourage fortement à vous lancer vous aussi dans la mise en place régulière de jeux avec vos élèves… je n’observe aucune perte de temps lorsque mes élèves jouent, et, au contraire, les savoir-faire mathématiques développés lors du jeu semblent encore plus solides.
Fabrice Bascou, Professeur de Mathématiques, à Nazareth, Nice
NDLR : Paroles d’élèves, recueillies après ces séances. Voici ce que Jules, Matthieu, Mattéo et Mathias m’ont confié :
C’est plus ludique, plus facile, parce qu’on le fait ensemble, on partage nos idées. On a chacun notre opinion, mais on peut en changer, grâce aux autres. Les rôles, ça permet d’aller plus vite, chacun sait ce qu’il a à faire, mais on n’est pas enfermé dans nos rôles…
Merci à toi, Fabrice, de m’avoir offert ces beaux cadeaux pédagogiques !!
Une très bonne émission, en ce jeudi 23 novembre, qui vient à point nommé renforcer les propos de Fabrice, dans son article de cette semaine.
A réécouter… clic sur l’image
TEMOIGNAGE (Part.1)
Je suis prof de maths au collège Nazareth de Nice. J’ai débuté ma carrière en 2002 avec les outils qu’un prof débutant peut avoir et j’avais donc l’image du prof sur son estrade qui transmet à ses élèves un savoir que lui seul possède…
L’expérience, la formation, les rencontres, les lectures et surtout un constat ont fait évoluer mes pratiques professionnelles : Demandez à des élèves en fin de CM2 quelle est leur matière préférée et posez la même question à des élèves en fin de 3ème… 😥
Je m’efforce donc de donner un maximum de sens et de rendre ludique les différentes activités proposées aux élèves afin que chacun, et même celui qui se trouve « nul », puisse y trouver un élément déclencheur de motivation, d’envie de chercher…
Je ne vous apprends rien si je vous dis que j’ai, du coup, changé ma posture et de ce fait celle des élèves ; en effet, de simples spectateurs ils deviennent acteurs de leurs apprentissages.
Il faut alors susciter chez eux l’envie de « chercher, modéliser, représenter, raisonner, calculer et communiquer ». « Pour ce faire, une place importante doit être accordée à la résolution de problèmes […] liés à des situations de la vie quotidienne […]. » (programme)
Approchez, j’ai une recette pour vous : une bonne tâche à prise d’initiative accompagnée d’un peu de pédagogie coopérative et c’est banco ! En effet, «Les activités exigeant une prise d’initiative sollicitent l’autonomie et l’imagination des élèves.» (ressources d’accompagnement)
J’ai demandé à Anne de venir observer une séance dans laquelle je propose aux élèves d’une classe de 4ème une tâche complexe afin d’ouvrir mes pratiques à un regard extérieur et avisé.
Il s’agit d’un problème de Dudu présenté dans une vidéo (à retrouver en cliquant sur l’image, aller à Pythagore, Saison 3- Episode 8, dans les problèmes ouverts)
Les Dudu sont deux frères profs de maths qui font un travail extraordinaire, vous trouverez sur leur blog une quantité incroyable de vidéos à exploiter en classe, dès la 6ème, (et pourquoi pas en CM2, avec un étayage plus soutenu, Ndlr)
Ndlr : Fabrice parle des Dudu, qui parlent de Fabrice !!, c’est ici.
La séance a commencé par un premier visionnage de la vidéo, les élèves sont invités à porter leur attention sur la situation de vie qui se déroule sous leurs yeux, et à commencer à noter quelques informations.
La vidéo est visionnée une seconde fois avec pour intention de récolter un maximum d’informations qui vont permettre de résoudre le problème des DUDU, ainsi chaque élève est invité à prendre des notes sur son cahier de recherche.
La situation était la suivante : Julien doit traiter la toiture de son préau contre les moisissures certainement, il a acheté un pot de produit permettant de couvrir 15 m2… son frère n’est pas d’accord !
La notion mathématique à mobiliser ici était le théorème de Pythagore.
J’ai laissé ensuite un temps de recherche individuel aux élèves afin qu’ils puissent commencer à réfléchir, trouver des pistes de réflexion, faire des figures, organiser leur prise de notes, se questionner…
Après ce temps, court mais important, de travail individuel, les élèves ont commencé à coopérer, échanger, mettre en commun, se poser des questions, se mettre d’accord, se contredire, convaincre, se laisser convaincre, afin qu’un raisonnement collectif se construise.
En tant qu’enseignant, il s’agit vraiment d’une phase de travail de la part des élèves agréable à observer. En effet, chaque élève semble oublier qu’il est en train de «faire des maths» !
Des rôles sont distribués lors d’un travail en coopération, le secrétaire rédige la trace de recherche sur une feuille qui sera elle-même présentée et commentée à travers un visualiseur au tableau par le rapporteur, les questions m’étant adressées sont uniquement posées par l’intermédiaire et enfin le gestionnaire gère le temps attribué et le niveau sonore.
J’avais prévu initialement une mise en commun du travail de chaque équipe : chaque rapporteur vient présenter son travail à la classe avec pour consigne d’apporter toujours une information nouvelle par rapport à ce qui a déjà été dit. Cela permet à chaque équipe d’apporter sa pierre à la mise en commun et surtout de gagner du temps sur celle-ci.
Concernant cette séance en particulier, je n’ai pas pu faire cette mise en commun, en effet le travail de recherche de la part des élèves a été plus long que prévu et je ne pouvais pas le stopper brutalement sous prétexte de timing. Cependant, sans rentrer dans les détails, nous avons fait une petite mise en commun intermédiaire : un cahier de recherche a été présenté à la classe à l’aide du visualiseur et la classe s’est mise d’accord sur ce qu’il fallait traiter comme information, et à quel “outil mathématique” cette situation faisait appel. Nous sommes donc là sur un premier écrit formatif, provisoire, qui ne demandera qu’à être complété, enrichi et rédigé.
La séance suivante finalisera et structurera les connaissances.
Et il ne fait aucun doute que lors de cette activité, les élèves ont effectué un réel travail de recherche : ils ont fait des essais, se sont posés des questions, ont testé des hypothèses, ont argumenté… Les 6 compétences mathématiques :
chercher, modéliser, représenter, raisonner, calculer et communiquer ont réellement été mises en œuvre sans négliger les compétences sociales et coopérative favorisées par le travail en groupes.
La semaine prochaine, rendez-vous pour une nouvelle activité sur Pythagore, une séance de jeu de l’oie !
Fabrice Bascou, professeur de mathématiques, au collège Nazareth, formateur ISFEC M2 MEEF.
De multiples jeux pour faire des maths au collège.
Classés dans un tableau selon la place qu’ils vont occuper dans la séquence :
(1) Pour introduire une notion
(2) Pour réinvestir une notion
(3) Pour développer des automatismes
(4) Jeu coopératif
(5) Jeu de plateau
clic sur l’image pour accéder aux ressources
De nombreuses matrices pour résoudre des problèmes ouverts aux cycles 2 et 3, transférables au cycle 4, voici comment les auteurs nous expliquent leur démarche :
“Le dispositif est très simple. Il a été pensé pour réconcilier les problèmes ouverts et les programmes.
- On crée des binômes
- On photocopie autant de séries de matrices que de binômes
- On résout collectivement la première matrice de la série
- On lance les élèves sur la série. La deuxième matrice, toujours très simple, permet de repérer les quelques binômes qui n’ont toujours pas compris la consigne.
- Le travail se poursuit en autonomie
- Pour la validation, on peut confier ce travail à un ou des élèves (en avance ou munis de calculatrice par exemple..)
- Un moment de partage des méthodes, des résultats ou des stratégies sur la matrice 4 ou 5 peut être envisagé au bout de 20 minutes
- La séance dure en général plus de 40 minutes et moins de 60 minutes.”
clic sur l’image pour accéder aux ressources
M@ths en-vie est un projet interdisciplinaire en français et mathématiques avec utilisation d’outils et ressources numériques (ordinateur, tablette, appareil photo numérique, blog ou site d’école, logiciels photo, internet…). Objectifs poursuivis, outre la coopération et la mutualisation d’outils, ancrer les mathématiques au réel afin d’améliorer la compréhension en résolution de problèmes et développer la perception des élèves sur les objets mathématiques qui nous entourent. La suite de la démarche et les outils déjà en ligne, ici.
😀 J’ai un vrai coup de coeur pour ce site en pensant à nos élèves pour lesquels il est si difficile de se faire des représentations visuelles, qui ne conçoivent pas les liens à faire entre la vie de tous les jours et les mathématiques, mais aussi pour ceux qui conceptualisent vite mais n’arrivent pas à expliquer leur démarche…
Je vous “renvoie” également ici au cas où vous n’auriez pas encore découvert les 33 recommandations qui accompagnent les nouveaux programmes de mathématiques et le dernier livre de Stella Baruck, ainsi que ses passionnantes interviews..
Egalement, par ici, pour des astuces sur les tables de multiplication et la super chaine Youtube de Mickaël Launay à laquelle vous pouvez vous abonner, c’est là. Et je n’oublie pas son livre, “Le grand roman des maths”, en lecture plaisir ou à visée pédagogique, c’est vous qui voyez !
Vous l’avez peut-être déjà expérimentée cette fameuse fête du “100ème” jour de classe. Sinon, ou si vous avez envie de savoir comment d’autres collègues s’en sont emparé, c’est ici.
“Dysmoi”, cet excellent site propose un article complet et documenté sur les incidences des troubles praxiques sur les activités de représentation/mesure, mais aussi sur la construction de l’invariance du nombre. Des explications claires et des pistes de travail à découvrir et à partager en équipe. Ici.
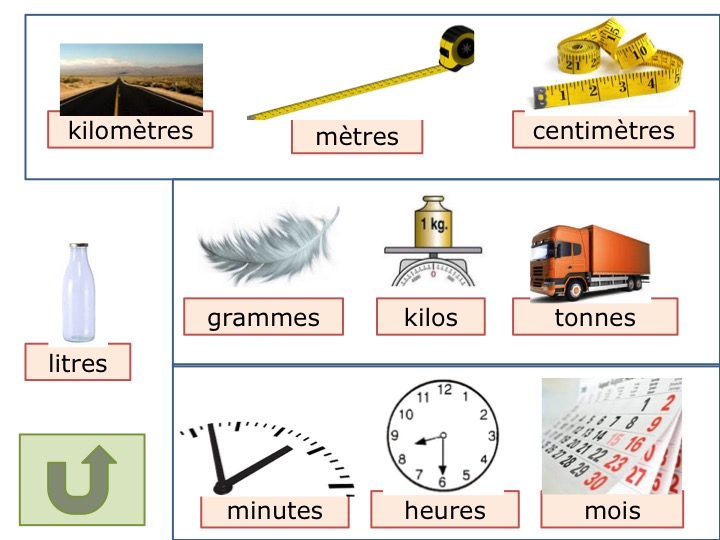Un diaporama sur les unités de mesure, c’est sur Pontt, et c’est à télécharger ici.
De nouveaux exercices sur la monnaie, à utiliser en complément d’une “vraie” manipulation, c’est sur Clic ma classe….
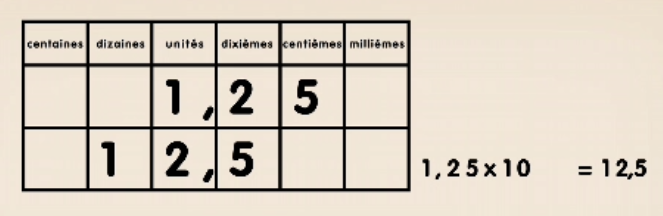A retrouver sur Canopé un nouveau film agité pour mieux cogiter sur la multiplication d’un décimal par 10, 100, 1000… pas mal fait !
Prenez un peu de temps et du calme pour lire cette publication et les multiples liens qui vous sont proposés. C’est passionnant et riche d’enseignement ! C’est ici.
Rémi Brissiaud nous livre deux textes tout à fait intéressants sur le programme de mathématiques en maternelle et notamment sur le comptage-dénombrement.
(A retrouver sur le site du Café, bien sûr)
Lorsque des élèves sont en difficulté importantes en maths, en CP ou en CE1, pourquoi ne pas aller chercher en amont ce qu’il a « construit » comme représentations du nombre ? Les surprises sont parfois de taille ! Et des ateliers de remédiation s’imposent !
Le nombre en maternelle
Une conférence de Stanislas Dehaene sur les fondements cognitifs de l’apprentissage des mathématiques à voir, ici
L’attention et le contrôle exécutif, autre conférence tout aussi éclairante, ici